Flat morphism

In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,

f_P: O_Y,f(P) → O_X,P

is a flat map for all P in X.^[1] f is a faithfully flat morphism if f is a surjective flat morphism.^[2]

Two of the basic intuitions are that flatness is a generic property, and that the failure of flatness occurs on the jumping set of the morphism.

The first of these comes from commutative algebra: subject to some finiteness conditions on f, it can be shown that there is a non-empty open subscheme Y′ of Y, such that f restricted to Y′ is a flat morphism (generic flatness). Here 'restriction' is interpreted by means of fiber product, applied to f and the inclusion map of Y′ into Y.

For the second, the idea is that morphisms in algebraic geometry can exhibit discontinuities of a kind that are detected by flatness. For instance, the operation of blowing down in the birational geometry of an algebraic surface, can give a single fiber that is of dimension 1 when all the others have dimension 0. It turns out (retrospectively) that flatness in morphisms is directly related to controlling this sort of semicontinuity, or one-sided jumping.

Flat morphisms are used to define (more than one version of) the flat topos, and flat cohomology of sheaves from it. This is a deep-lying theory, and has not been found easy to handle. The concept of étale morphism (and so étale cohomology) depends on the flat morphism concept: an étale morphism being flat, of finite type, and unramified.

1 Properties of flat morphisms
2 Notes
3 References

Properties of flat morphisms

Let f : X → Y be a morphism of schemes. For a morphism g : Y′ → Y, let X′ = X ×_Y Y′ and f′ = f × g : X′ → Y′. f is flat if and only if for every g, the pullback f′^* is an exact functor from the category of quasi-coherent 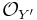$\mathcal{O}_{Y'}$ -modules to the category of quasi-coherent 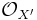$\mathcal{O}_{X'}$ -modules.^[3]

Assume that f : X → Y and g : Y → Z are morphisms of schemes. Assume furthermore that f is flat at x in X. Then g is flat at f(x) if and only if gf is flat at x.^[4] In particular, if f is faithfully flat, then g is flat or faithfully flat if and only if gf is flat or faithfully flat, respectively.^[5]

Fundamental properties

The composite of two flat morphisms is flat.^[6]
The fibered product of two flat or faithfully flat morphisms is a flat or faithfully flat morphism, respectively.^[7]
Flatness and faithful flatness is preserved by base change: If f is flat or faithfully flat and g : Y′ → Y, then the fiber product f × g : X ×_Y Y′ → Y′ is flat or faithfully flat, respectively.^[8]
The set of points where a morphism (locally of finite presentation) is flat is open.^[9]
If f is faithfully flat and of finite presentation, and if gf is finite type or finite presentation, then g is of finite type or finite presentation, respectively.^[10]

Suppose that f: X → Y is a flat morphism of schemes.

If F is a quasi-coherent sheaf of finite presentation on Y (in particular, if F is coherent), and if J is the annihilator of F on Y, then 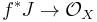$f^*J \to \mathcal{O}_X$ , the pullback of the inclusion map, is an injection, and the image of f^*J in 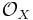$\mathcal{O}_X$ is the annihilator of f^*F on X.^[11]
If f is faithfully flat and if G is a quasi-coherent 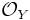$\mathcal{O}_Y$ -module, then the pullback map on global sections 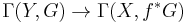$\Gamma(Y, G) \to \Gamma(X, f^*G)$ is injective.^[12]

Suppose now that h : S′ → S is flat. Let X and Y be S-schemes, and let X′ and Y′ be their base change by h.

If f : X → Y is quasi-compact and dominant, then its base change f′ : X′ → Y′ is quasi-compact and dominant.^[13]
If h is faithfully flat, then the pullback map Hom_S(X, Y) → Hom_S′(X′, Y′) is injective.^[14]
Assume that f : X → Y is quasi-compact and quasi-separated. Let Z be the closed image of X, and let j : Z → Y be the canonical injection. Then the closed subscheme determined by the base change j′ : Z′ → Y′ is the closed image of X′.^[15]

Topological properties

If f : X → Y is flat, then it possesses all of the following properties:

For every point x of X and every generization y′ of y = f(x), there is a generization x′ of x such that y′ = f(x′).^[16]
For every point x of X, 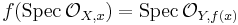$f(\operatorname{Spec}\,\mathcal{O}_{X,x}) = \operatorname{Spec}\,\mathcal{O}_{Y,f(x)}$ .^[17]
For every irreducible closed subset Y′ of Y, every irreducible component of f⁻¹(Y′) dominates Y.^[18]
If Z and Z′ are two irreducible components of Y with Z contained in Z′, then for every irreducible component T of f⁻¹(Z), there is an irreducible component T′ of f⁻¹(Z′) containing T.^[19]
For every irreducible component T of X, the closure of f(T) is an irreducible component of Y.^[20]
If Y is irreducible with generic point y, and if f⁻¹(y) is irreducible, then X is irreducible.^[21]
If f is also closed, the image of every connected component of X is a connected component of Y.^[22]
For every pro-constructible subset Z of Y, 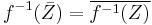$f^{-1}(\bar Z) = \overline{f^{-1}(Z)}$ .^[23]

If f is flat and locally of finite presentation, then f is universally open.^[24] However, if f is faithfully flat and quasi-compact, it is not in general true that f is open, even if X and Y are noetherian.^[25] Furthermore, no converse to this statement holds: If f is the canonical map from the reduced scheme X_red to X, then f is a universal homeomorphism, but for X noetherian, f is never flat.^[26]

If f : X → Y is faithfully flat, then:

The topology on Y is the quotient topology relative to f.^[27]
If f is also quasi-compact, and if Z is a subset of Y, then Z is a locally closed pro-constructible subset of Y if and only if f⁻¹(Z) is a locally closed pro-constructible subset of X.^[28]

If f is flat and locally of finite presentation, then for each of the following properties P, the set of points where f has P is open:^[29]

Serre's condition S_k (for any fixed k).
Geometrically regular.
Geometrically normal.

If in addition f is proper, then the same is true for each of the following properties:^[30]

Geometrically reduced.
Geometrically reduced and having k geometric connected components (for any fixed k).
Geometrically integral.

Flatness and dimension

Assume that X and Y are locally noetherian, and let f : X → Y.

Let x be a point of X and y = f(x). If f is flat, then dim_x X = dim_y Y + dim_x f⁻¹(y).^[31] Conversely, if this equality holds for all x, X is Cohen-Macaulay, and Y is regular, then f is flat. ^[32]
If f is faithfully flat, then for each closed subset Z of Y, codim_Y(Z) = codim_X(f⁻¹(Z)).^[33]
Suppose that f is flat and that F is a quasi-coherent module over Y. If F has projective dimension at most n, then f^*F has projective dimension at most n.^[34]

Descent properties

Assume f is flat at x in X. If X is reduced or normal at x, then Y is reduced or normal, respectively, at f(x).^[35] Conversely, if f is also of finite presentation and f⁻¹(y) is reduced or normal, respectively, at x, then X is reduced or normal, respectively, at x.^[36]
In particular, if f is faithfully flat, then X reduced or normal implies that Y is reduced or normal, respectively. If f is faithfully flat and of finite presentation, then all the fibers of f reduced or normal implies that X is reduced or normal, respectively.
If f is flat at x in X, and if X is integral or integrally closed at x, then Y is integral or integrally closed, respectively, at f(x).^[37]
If f is faithfully flat, X is locally integral, and the topological space of Y is locally noetherian, then Y is locally integral.^[38]
If f is faithfully flat and quasi-compact, and if X is locally noetherian, then Y is also locally noetherian.^[39]
Assume that f is flat and X and Y are locally noetherian. If X is regular at x, then Y is regular at f(x). Conversely, if Y is regular at f(x) and f⁻¹(f(x)) is regular at x, then X is regular at x.^[40]
Assume again that f is flat and X and Y are locally noetherian. If X is normal at x, then Y is normal at f(x). Conversely, if Y is normal at f(x) and f⁻¹(f(x)) is normal at x, then X is normal at x.^[41]

Let g : Y′ → Y be faithfully flat. Let F be a quasi-coherent sheaf on Y, and let F′ be the pullback of F to Y′. Then F is flat over Y if and only if F′ is flat over Y′.^[42]

Assume that f is faithfully flat and quasi-compact. Let G be a quasi-coherent sheaf on Y, and let F denote its pullback to X. Then F is finite type, finite presentation, or locally free of rank n if and only if G has the corresponding property.^[43]

Suppose that f : X → Y is an S-morphism of S-schemes. Let g : S′ → S be faithfully flat and quasi-compact, and let X′, Y′, and f′ denote the base changes by g. Then for each of the following properties P, f has P if and only if f′ has P.^[44]

Open.
Universally open.
Closed.
Universally closed.
A homeomorphism.
A universal homeomorphism.
Quasi-compact.
Quasi-compact and universally bicontinuous.
Quasi-compact and a homeomorphism onto its image.
Quasi-compact and dominant.
Separated.
Quasi-separated.
Locally of finite type.
Locally of finite presentation.
Finite type.
Finite presentation.
Proper.
An isomorphism.
A monomorphism.
An open immersion.
A quasi-compact immersion.
A closed immersion.
Affine.
Quasi-affine.
Finite.
Quasi-finite.
Integral.

It is possible for f′ to be a local isomorphism without f being even a local immersion.^[45]

If f is quasi-compact and L is an invertible sheaf on X, then L is f-ample or f-very ample if and only if its pullback L′ is f′-ample or f′-very ample, respectively.^[46] However, it is not true that f is projective if and only if f′ is projective. It is not even true that if f is proper and f′ is projective, then f is quasi-projective, because it is possible to have an f′-ample sheaf on X′ which does not descend to X.^[47]

Notes

^ EGA IV₂, 2.1.1.
^ EGA 0_I, 6.7.8.
^ EGA IV₂, Proposition 2.1.3.
^ EGA IV₂, Corollaire 2.2.11(iv).
^ EGA IV₂, Corollaire 2.2.13(iii).
^ EGA IV₂, Corollaire 2.1.6.
^ EGA IV₂, Corollaire 2.1.7, and EGA IV₂, Corollaire 2.2.13(ii).
^ EGA IV₂, Proposition 2.1.4, and EGA IV₂, Corollaire 2.2.13(i).
^ EGA IV₃, Théorème 11.3.1.
^ EGA IV₃, Proposition 11.3.16.
^ EGA IV₂, Proposition 2.1.11.
^ EGA IV₂, Corollaire 2.2.8.
^ EGA IV₂, Proposition 2.3.7(i).
^ EGA IV₂, Corollaire 2.2.16.
^ EGA IV₂, Proposition 2.3.2.
^ EGA IV₂, Proposition 2.3.4(i).
^ EGA IV₂, Proposition 2.3.4(ii).
^ EGA IV₂, Proposition 2.3.4(iii).
^ EGA IV₂, Corollaire 2.3.5(i).
^ EGA IV₂, Corollaire 2.3.5(ii).
^ EGA IV₂, Corollaire 2.3.5(iii).
^ EGA IV₂, Proposition 2.3.6(ii).
^ EGA IV₂, Théorème 2.3.10.
^ EGA IV₂, Théorème 2.4.6.
^ EGA IV₂, Remarques 2.4.8(i).
^ EGA IV₂, Remarques 2.4.8(ii).
^ EGA IV₂, Corollaire 2.3.12.
^ EGA IV₂, Corollaire 2.3.14.
^ EGA IV₃, Théorème 12.1.6.
^ EGA IV₃, Théorème 12.2.4.
^ EGA IV₂, Corollaire 6.1.2.
^ EGA IV₂, Proposition 6.1.5. Note that the regularity assumption on Y is important here. The extension $\mathbb C[x^2, y^2, xy]\subset \mathbb C[x,y]$ gives a counterexample with X regular, Y normal, f finite surjective but not flat.
^ EGA IV₂, Corollaire 6.1.4.
^ EGA IV₂, Corollaire 6.2.2.
^ EGA IV₂, Proposition 2.1.13.
^ EGA IV₃, Proposition 11.3.13.
^ EGA IV₂, Proposition 2.1.13.
^ EGA IV₂, Propostion 2.1.14.
^ EGA IV₂, Proposition 2.2.14.
^ EGA IV₂, Corollaire 6.5.2.
^ EGA IV₂, Corollaire 6.5.4.
^ EGA IV₂, Proposition 2.5.1.
^ EGA IV₂, Proposition 2.5.2.
^ EGA IV₂, Proposition 2.6.2, Corollaire 2.6.4, and Proposition 2.7.1.
^ EGA IV₂, Remarques 2.7.3(iii).
^ EGA IV₂, Corollaire 2.7.2.
^ EGA IV₂, Remarques 2.7.3(ii).

References

Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1; 978-0-387-94269-8, MR 1322960 , section 6.
Serre, Jean-Pierre (1956), "Géométrie algébrique et géométrie analytique", Université de Grenoble. Annales de l'Institut Fourier 6: 1–42, ISSN 0373-0956, MR 0082175, http://www.numdam.org/numdam-bin/item?id=AIF_1956__6__1_0
Grothendieck, Alexandre; Dieudonné, Jean (1960). "Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) : I. Le langage des schémas". Publications Mathématiques de l'IHÉS 4. MR 0217083. http://www.numdam.org:80/numdam-bin/feuilleter?id=PMIHES_1960__4_.
Grothendieck, Alexandre; Dieudonné, Jean (1965). "Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) : IV. Étude locale des schémas et des morphismes de schémas, Seconde partie". Publications Mathématiques de l'IHÉS 24. MR 0199181. http://www.numdam.org:80/numdam-bin/feuilleter?id=PMIHES_1965__24_.
Grothendieck, Alexandre; Dieudonné, Jean (1966). "Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) : IV. Étude locale des schémas et des morphismes de schémas, Troisième partie". Publications Mathématiques de l'IHÉS 28. MR 0217086. http://www.numdam.org:80/numdam-bin/feuilleter?id=PMIHES_1966__28_.
Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics, 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157